An Introduction to Multiple Linear Regression (MLR) in R
Blog Tutorials
Discover the essentials of multiple linear regression in R, through a practical “Performance Index” dataset.
An Introduction to Multiple Linear Regression (MLR) in R
What Is Predictive Modelling?
Predictive modeling involves creating a statistical model to predict or estimate the probability of an outcome. These models are typically developed using historical or purposely collected data. Predictive analytics has applications across many domains, including finance, insurance, telecommunications, retail, healthcare, and sports.
Predictive Modeling – General Approach
Setting the Business Goal
Data Understanding and Pre-Processing
Exploratory Data Analysis
Developing Statistical Model
Model Evaluation and Validation
Model Implementation

Multiple Linear Regression Introduction
Multiple linear regression (MLR) is used to explain the relationship between one continuous dependent variable and two or more independent variables, which can be continuous or categorical. The variable we want to predict (or model) is called the dependent variable, while the independent variables (also known as explanatory variables or predictors) are those used to predict the outcome.
Example: If the goal is to predict a house’s price (dependent variable), potential independent variables could include its area, location, air quality index, or distance from the airport.
Multiple Linear Regression: Statistical Model
Y=β0+β1X1+β2X2+⋯+βpXp+ϵ
Y: Dependent variable
X1,X2,…,Xp: Independent variables
β0,β1,…,βp: Parameters (coefficients)
ϵ: Random error component
MLR requires that the model be linear in the parameters (though the predictors themselves can be numeric or categorical). Parameter estimates are often found using the Least Squares Method, which minimizes the sum of squared residuals.
Case Study – Modeling Job Performance Index
This case study uses a dataset called Performance Index, containing:
jpi: Job Performance Index (dependent variable)
aptitude: Aptitude test score
tol: Test of language score
technical: Technical knowledge score
general: General information score

Data Snapshot

Columns | Description | Type | Measurement | Possible values |
|---|---|---|---|---|
empid | Employee ID | integer | - | - |
jpi | Job performance Index | numeric | - | positive values |
aptitude | Aptitude score | numeric | - | positive values |
tol | Test of Language | numeric | - | positive values |
technical | Technical Knowledge | numeric | - | positive values |
general | General Information | numeric | - | positive values |

Below is a snippet of how we might load and inspect the dataset in R.
Parameter Estimation Using the Least Squares Method
Parameters | Coefficients |
|---|---|
Intercept | -54.2822 |
aptitude | 0.3236 |
tol | 0.0334 |
technical | 1.0955 |
general | 0.5368 |
If we denote Job Performance Index as jpi, then one possible model from the data is:
Parameter Estimation Using lm() in R
Model Fit
Output

Interpretation of Partial Regression Coefficients
Each coefficient βi tells us how much jpi changes with a one-unit increase in the corresponding predictor, holding all other variables constant. For instance, if the coefficient for aptitude is 0.3236, then a 1-point increase in the aptitude score (assuming everything else is fixed) increases the job performance index by 0.3236.
Individual Testing – Using t Test
To test which variables are significant:
Null Hypothesis (H0): βi=0
Alternate Hypothesis (H1): βi≠0
The summary(model) output provides p-values for each coefficient. Typically, a p-value < 0.05 suggests that the variable is significant.
Parameters | Coefficients | Standard Error | t statistic | p-value |
|---|---|---|---|---|
Intercept | -54.2822 | 7.3945 | -7.3409 | 0.0000 |
aptitude | 0.3236 | 0.0678 | 4.7737 | 0.0001 |
tol | 0.0334 | 0.0712 | 0.4684 | 0.6431 |
technical | 1.0955 | 0.1814 | 6.0395 | 0.0000 |
general | 0.5368 | 0.1584 | 3.3890 | 0.0021 |
Measure of Goodness of Fit – R^2
R^2 indicates the proportion of variation in the dependent variable (jpi) explained by the independent variables. Higher R^2 values imply a better fit. An adjusted R^2 also accounts for the number of predictors in the model.
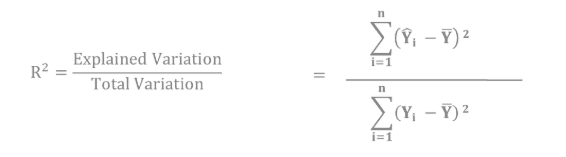
The adjusted R-squared is a modified version of R-squared that has been adjusted for the number of predictors in the modelling.

Summary Output
Significant variables are aptitude, technical, and general since their p-values are < 0.05.
Insignificant variable is tol, as its p-value exceeds 0.05.
An R-squared of 0.88 suggests that 88% of the variation in job performance is explained by these predictors.
Interpretation: Increasing
aptitudeby 1 unit, while holding other variables constant, increasesjpiby approximately its parameter estimate. The same logic applies totechnicalandgeneral.
Fitted Values and Residuals
Once you have the estimated model, you can compute fitted values and residuals:
Adding Fitted Values and Residuals to the Original Dataset

Predictions for a New Dataset
When you have new data with the same independent variables, you can generate predictions:

Important: Ensure that the new dataset has all the independent variables used in the model, with matching column names.
Multiple Linear Regression: Assumptions & Diagnostics
We built a multiple linear regression model to predict jpi (Job Performance Index) from four predictors in the Performance Index dataset:
aptitudetol(test of language)technicalgeneral
In this continuation, we will check the assumptions of multiple linear regression—multicollinearity and the normality of errors—and illustrate residual analysis techniques. Such checks are essential to ensure valid model interpretations and reliable predictions.
Problem of Multicollinearity
Multicollinearity arises when two or more independent variables in a regression model exhibit a strong linear relationship. This leads to:
Highly unstable model parameters: The standard errors of the coefficients become inflated, making them unreliable.
Potentially poor out-of-sample predictions: The model might fail to generalize accurately.
Hence, detecting and handling multicollinearity is an important step in regression.
Detecting Multicollinearity Through VIF
The Variance Inflation Factor (VIF) is a common way to detect multicollinearity. A VIF > 5 (some use a threshold of 10) can indicate problematic multicollinearity.

Detecting Multicollinearity in R

If one or more VIF values exceed 5, you are likely dealing with multicollinearity.
Multicollinearity – Remedial Measures
Possible solutions include:
Removing one or more correlated independent variables
Combining correlated predictors via dimensionality reduction (e.g., Principal Component Analysis)
Collecting more data to stabilize parameter estimates
Residual Analysis
Residuals represent the difference between the observed and predicted values:
Residual = Observed Value−Predicted Value
A thorough residual analysis is vital for checking assumptions:
Errors follow a Normal Distribution (Normality of errors)
Homoscedasticity (Constant variance of residuals)
No obvious patterns or autocorrelation
Normality of Errors
Multiple linear regression assumes that the errors (residuals) follow a normal distribution. If this assumption is severely violated, the p-values and confidence intervals (based on t and F distributions) can become unreliable.
Residual Analysis for the Performance Index Data
Continuing with our Performance Index model:
Get the fitted values and residuals.
Analyze their distribution.
Residual v/s Predicted Plot in R
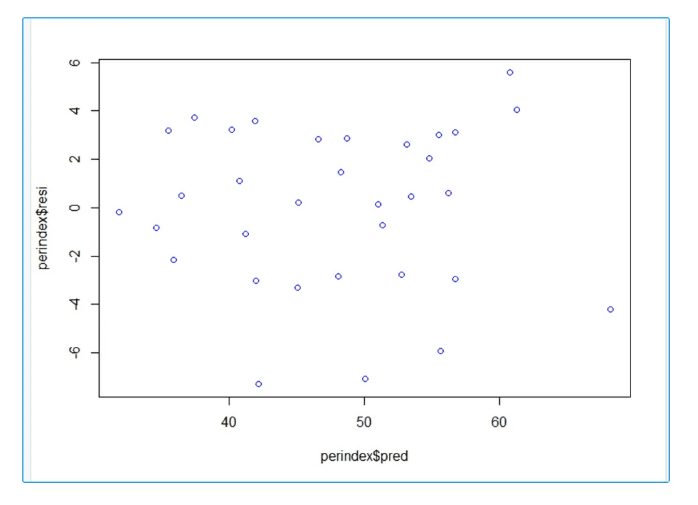
Interpretation:
Residuals in our model are randomly distributed which indicates presence of Homoscedasticity
A random scatter around zero is generally good; patterns or funnel-shaped spreads can indicate issues like heteroscedasticity or non-linearity.
Normality Checks
Q-Q Plot
Shapiro-Wilk Test
Kolmogorov-Smirnov (KS) Test
Q-Q Plot
The Q-Q plot compares sample quantiles of the residuals to the theoretical quantiles of a normal distribution. If points lie roughly on a straight line, the errors are likely normally distributed.

Interpretation:
Most of these points are close to the line except few values indicating no serious deviation from Normality.
Shapiro-Wilk Test
A p-value > 0.05 suggests we do not reject the hypothesis that the residuals are normally distributed.
Absence of Normality – Remedial Measures
If the residuals are not normally distributed, we can apply transformations to the dependent variable, such as a log transform. More generally, a Box-Cox transformation can be used, where R will attempt to find an optimal exponent (λ\lambda).
Box Cox transformation

Conclusion
In this blog, we used multiple linear regression to analyze the Performance Index dataset. We:
Explored the data and fit a linear model using
lm().Evaluated coefficients, significance (via t-tests), and model fit using R2R^2.
Generated predictions for both the existing data (fitted values) and a new dataset.
Check Multicollinearity: Calculate VIFs. If >5, consider removing or combining problematic variables.
Residual Analysis: Plot Residuals vs. Fitted to confirm no major patterns.
Normality of Errors: Generate Q-Q plot and run tests (Shapiro-Wilk). If violated, try a transformation.
By following these steps—business understanding, data exploration, model building, and evaluation—you can create robust predictive models to inform data-driven decisions.
By examining multicollinearity (via VIF) and residuals (via diagnostic plots and normality tests), you ensure that the multiple linear regression model for the Performance Index data remains trustworthy. Addressing issues like high correlation among predictors or non-normal errors can greatly improve the model’s reliability and predictive power.
